IVFFlat vs. HNSW - and how to use them in Amazon DocumentDB
Learn about he most popular vector search indexes, IVFFlat and HNSW, and how to use them in DocumentDB turning into a really capable vector database.
Published Mar 14, 2024
Last year during re:Invent 2023, AWS released the ability to do use DocumentDB, AWS’s MongoDB-compatible JSON-native document database, as a vector database.
To being with it only supported the IVFFlat indexing algorithm, but now it has also released support for HSNW. Let’s first cover some basic differences and then I’ll show you how easy it is to create a vector index of either type on DocumentDB.
IVFFlat stands for Inverted File with Flat Compression. This has been one of the mainstream algorithms for a long time and is a go-to when you’ve got limited resources because it has low memory usage and fast index build time.
Basically, it works by using an indexing algorithms to go through all the vector data stored and group them into different clusters based on how similar they are to each other. It then calculates what is called a centroid vector for each cluster which determines the entry point, if you will, into that cluster. Then, once a query is sent to the index it will perform a similarity search between this query vector and the centroids to identify which cluster has the best response. It will then look into that cluster for the answer and return the relevant vector.
Because of this training step required before your index can be built you must have some vector data stored already before you can use IVFFlat. There is no set recommendation, however, a substantial amount is ideal which means anything starting from at least several thousands of data points.
The other thing to take into consideration is that as vectors are added, deleted, updated, etc in the database the IVFFlat index will add them to whichever of these pre-trained clusters seem to be the best match. This, of course, can lead to a degradation of relevancy leading to poorer results over time if your datasets have a lot of change.
So to maintain quality you may want to re-build the index regularly if you expect a lot of data updates. This could be costly and possibly also interfere with your business-as-usual (BAU) operations as you’d have to measure the impact on your database while the index is being rebuilt. On the plus side, this training step where data is separated into clusters is a fairly simple process and also very efficient so the build time for the index is actually quite fast.
Hierarchical Navigable Small Worlds, HNSW for short, is another very popular vector indexing algorithm and the first main advantage over IVFFlat is that you don’t need to have any data to get started.
HNSW is quite straightforward on the face of it. It effectively mixes two concepts: skip lists and Navigable Small Worlds.
The data structure enthusiasts out there may have heard of skip lists which are a specialization of linked lists, which traditionally taught in computer science courses. Instead of moving from one item to another sequentially like in a link list, a skip list adds one more piece of metadata to each node that allows you to skip around the list when processing it. Think like those number guessing games where you ask a question like “is it greater than 10?” and then someone says yes so you skip from your guess of 1 to something like 15 for your next shot.
Navigatable Small Worlds is a graph structure which is very efficient for ANN (Approximate Near Neighbor) search because the vertices are connected to others forming something of social media graph pattern where you can determine easily which vectors are “buddies” and “close buddies” with each other.
HNSW brings those two concepts together but adds multiple layers to the NSW graph structure, hence the Hierarchical addition to the name. When you create an hnsw index the database will create a co-relation between the field storing the vectors and this multi-layered graph index and from then it will work out the relationships between any new vectors or updated vectors as it goes.
Because of this, unlike IVFFlat, you don’t need to have any data to build the index. HNSW is very rellisient to data changes since it doesn’t have that training step like IVFFlat which needs to keep re-aligning the centroids. While HNSW indexes do take longer much longer to build (some benchmarks show a difference of 32x slower to build than IVFFlat), the good news is that you may not have to do it very often if at all unless you really do have huge volumes of changes that may warrant it. However, HNSW indexes have proven to be extremely resilient to degradation and even very frequent data changes may not have much of a significant impact, so you just have to monitor and decide what would be right for you.
Another thing to consider with HNSW is that it does not handle duplicate vectors very well resulting a exhaustive searches at the time the vectors are added or during query results. So if your datasets contain a lot of duplicate data you want to either sanitize them as part of a data pipeline before importing them into your HNSW index or skip indexing altogether.
pros:
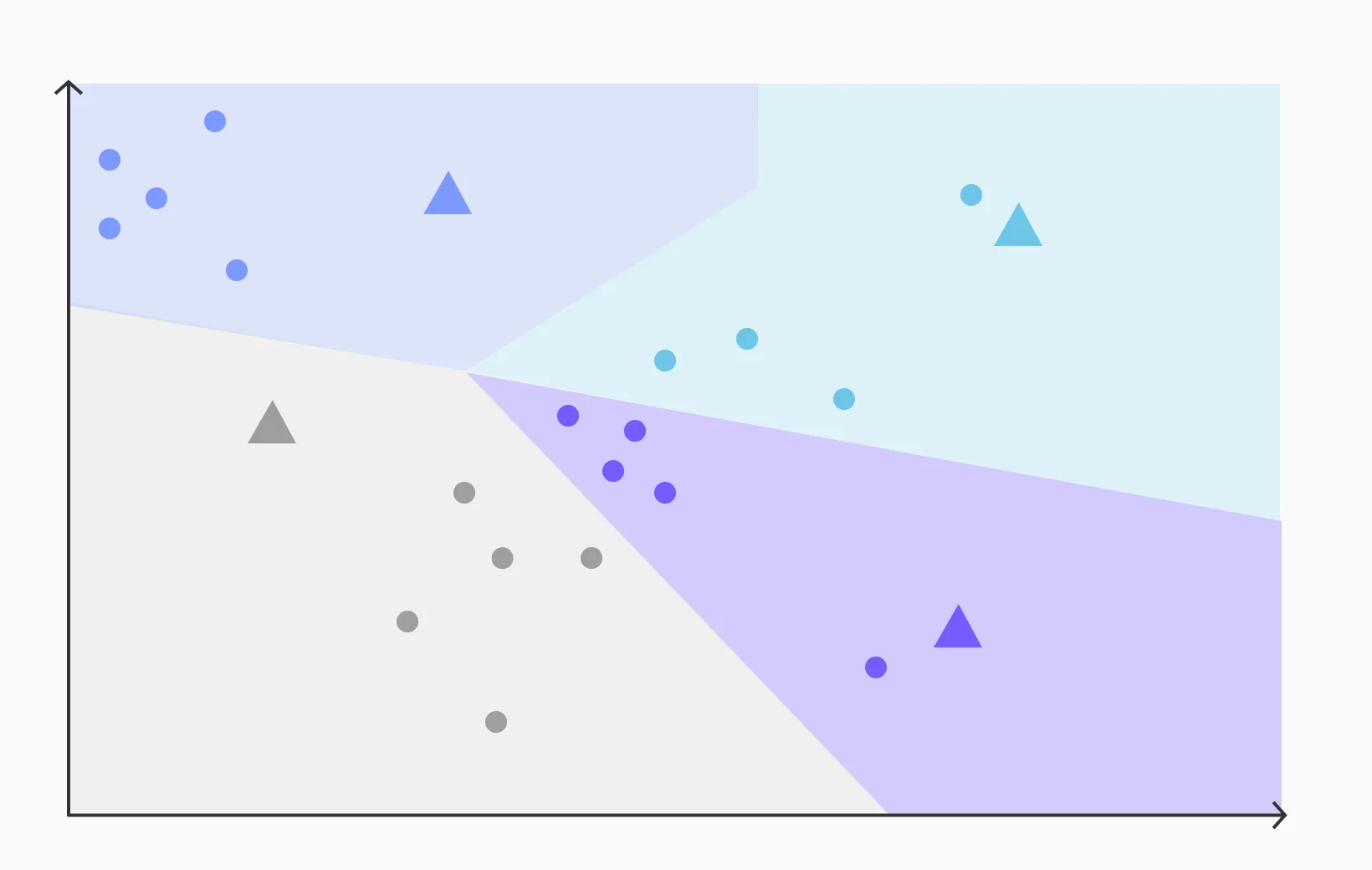
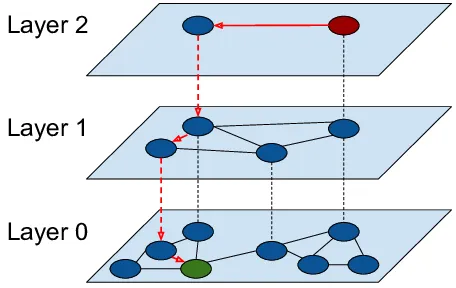
- Very fast built time
- Small storage size
- Low memory requirements
cons:
- Slower to generate responses
- quality of results deteriorates easily with data updates needing frequent rebuilding of the index
- Needs a substantial amount of data before you can create an IVFFlat index (several thousands of data points at minimum is recommended)
pros:
- Very fast (some benchmarks put it at a bit over 15x better than IVFFlat for response times)
- Very resillient to data updates with negligible impact on recall (that is the quality of relevance of results don’t degrade easily)
- No need for any data at all. You can create the index and populate it over time with very little impact
cons:
- Build time is significantly slower than IVFFlat (some benchmarks demonstrate that it can be 32x times slower) … but you may not need to rebuild the index very frequently if at all
- Needs more memory to run
- Has a bigger size in storage than an IVFFlat index (nearly triple the size according to some benchmarks)
And now for the easy part. That’s right, you thought creating the index would be the difficult bit? Nope, it’s as easy as issuing the create_index() command.
As you can see the command is pretty straightforward. It does have a few options that will impact things like performance, recall, resources needed, but these are things that you can play with until you discover which options are best for you as you dive deeper into vector search.
The important thing is to notice is that all of that theory about IVFFlat and HNSW is abstracted away from you by DocumentDB. All you need to do is choose which type of index you want to create by setting the “type” field in the vector options to either “hnsw” or “ivfflat” and you’re done.
Here’s an example of creating an IVFFlat index:
And here’s one of creating a HNSW index:
I hope this helps you get started into the exciting world of vector search! 😊