Community | GenAI under the hood [Part 5] - Matryoshka dolls and Embedding Vectors

Introduction

Most of us are familiar with the delightful Russian nesting dolls, known as Matryoshka dolls. These wooden dolls have a unique design where smaller dolls are nested within larger ones, creating a captivating display of concentric layers. While these dolls may have initially seemed like mere toys, their intrinsic design has inspired an innovative approach to representation learning in the field of machine learning, aptly named Matryoshka Representation Learning (MRL).

MRL draws its inspiration from the nested nature of Matryoshka dolls, aiming to create multi-granular representations that can adapt to various downstream tasks and computational constraints. Just as the smaller dolls are neatly tucked within the larger ones, MRL encodes information at different granularities within a single high-dimensional embedding vector.

One of the nice aspects of Matryoshka Representation Learning (MRL) is its ability to maintain high accuracy even when the learned representations are truncated to lower dimensions. This property is a direct consequence of the training process, where the loss function is explicitly optimized for a set of nested dimensions within the full embedding space.

How MRL representations are created

During training, MRL ensures that the information encoded in the lower-dimensional subspaces is as rich and discriminative as independently trained low-dimensional representations. This is achieved by carefully optimizing the multi-scale objective function, which encourages the model to distribute relevant information across the different granularities of the embedding vector. Consequently, when the Matryoshka Representation is truncated to a lower dimension, the resulting subspace retains a significant portion of the representational power, enabling accurate performance on downstream tasks without the need for retraining or additional computational overhead.

At its core, MRL modifies the standard representation learning pipeline by optimizing a multi-scale objective function. Instead of solely optimizing for the full embedding dimensionality, the loss function is also optimized for a set of lower dimensions chosen in a nested logarithmic fashion, such as 8, 16, 32, ..., 2048 dimensions for a 2048-dimensional embedding.

This approach introduces a unique set of parameters that can influence the accuracy of the representations at each granularity level.

One crucial parameter is the choice of the nested dimensions themselves. While MRL typically selects dimensions in a logarithmic spacing, inspired by the behavior of accuracy saturation across dimensions, the initial granularity and the spacing between dimensions can be tuned to achieve better performance.
Another parameter that can be adjusted is the weighting of the nested losses. By carefully balancing the importance of each nested dimension during the optimization process, MRL can potentially improve the accuracy of lower-dimensional representations without compromising the accuracy of higher-dimensional ones.

In code...

Here is some heavily commented code explaining MRL, inspired by the paper (source below) for those of you who are interested.

Code walkthrough

The MultiGranularityLoss class takes a list of granularity levels (e.g., [8, 16, 32, ..., 2048]) and a loss function (e.g., CrossEntropyLoss). During the forward pass, it calculates the loss for each granularity level and combines them using the provided granularity weights (or equal weights if none are provided).

The MultiGranularityClassifier class takes the same list of granularity levels and the number of classes. It has two implementations: efficient and non-efficient. In the efficient implementation, a single linear layer is shared across all granularity levels, and the input tensor is sliced accordingly before passing it through the layer. In the non-efficient implementation, separate linear layers are created for each granularity level, and the input tensor is passed through each layer separately.

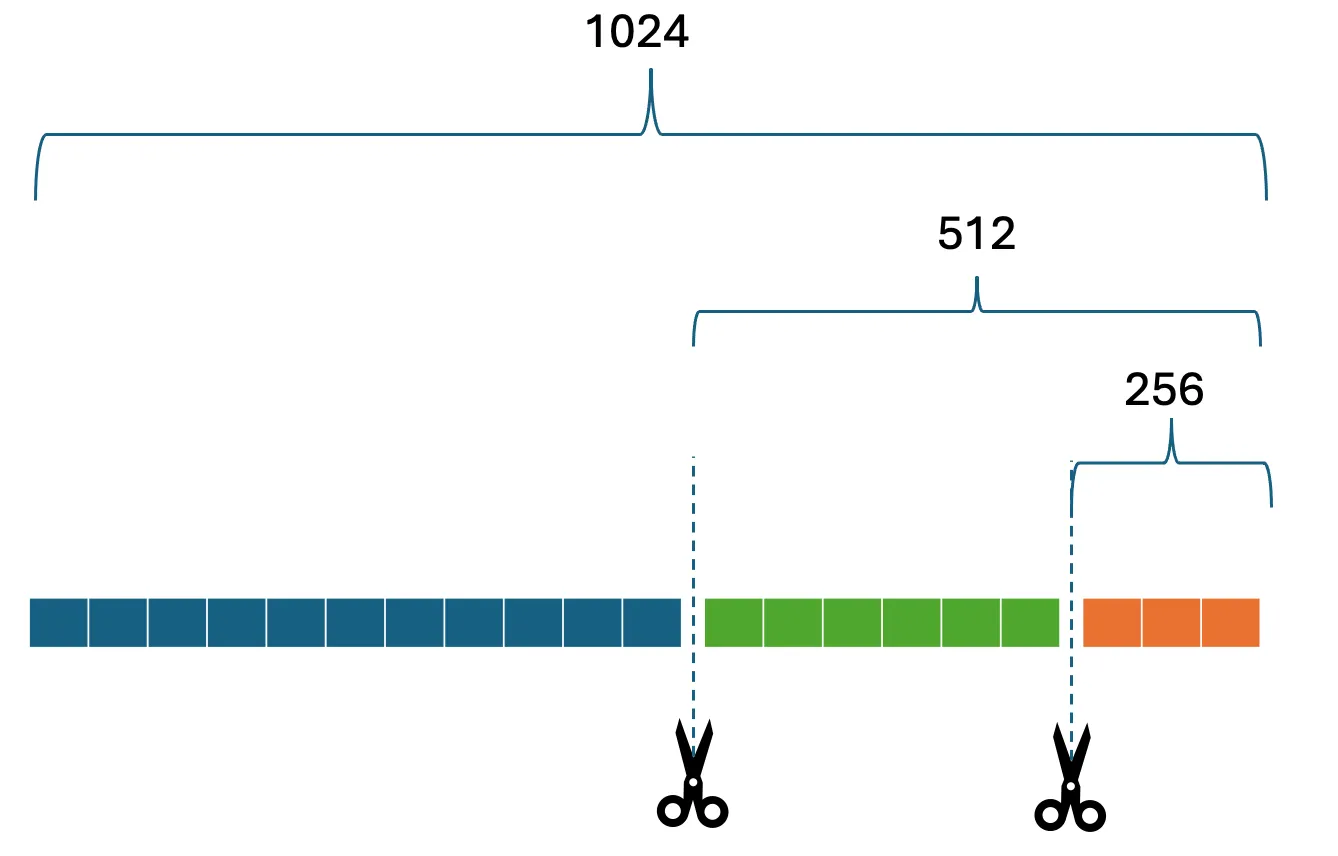
During the forward pass, the MultiGranularityClassifier returns a tuple of outputs, one for each granularity level. These outputs can then be used for various tasks, such as classification, retrieval, or adaptive deployment.

Ok I'm sold, how do I use this?

Several model providers now provide these nested embeddings. Amazon Text Embeddings V2 is a light weight, efficient model ideal for high accuracy retrieval tasks at different dimensions. The model supports flexible embeddings sizes (256, 512, 1,024) and prioritizes accuracy maintenance at smaller dimension sizes, helping to reduce storage costs without compromising on accuracy. When reducing from 1,024 to 512 dimensions, Titan Text Embeddings V2 retains approximately 99% retrieval accuracy, and when reducing from 1,024 to 256 dimensions, the model maintains 97% accuracy. Additionally, Titan Text Embeddings V2 includes multilingual support for 100+ languages in pre-training as well as unit vector normalization for improving accuracy of measuring vector similarity.

Let's start with a haiku (generated by Claude Haiku on Amazon Bedrock) about MRL, because, why not:

We can use Amazon Bedrock's new model to retrieve embeddings of 1024 and 512 dimensions given this input text:

Printing out these dimensions shows we have very different numbers:

Normalized vectors across different dimensions are expected to be different. Let us use the first 512 numbers from emb_1024, renormalize and then check again:

Now let's check v1 and v2:

That's almost the same. How different are these vectors? Let's output the mean absolute percentage error:

A very low MAPE will translate to low representation accuracy loss, but an end-to-end test needs to be done in production to make sure where you land, for example when using the model in RAG pipelines.

Of the several applications of Matryoshka Representations are one notable use is in adaptive classification, where lower-dimensional representations can be used for easy examples, allowing for early exits and saving computational resources. Another exciting application is efficient large-scale retrieval, where coarse retrieval can be performed using low-dimensional representations, followed by re-ranking with higher-dimensional representations. This approach, termed "adaptive retrieval" or "funnel retrieval," can lead to significant computational savings without sacrificing accuracy.

If you're interested in leveraging Matryoshka Representations for efficient retrieval or adaptive classification, here are the high-level steps you can follow:

Train a model using the Matryoshka Representation Learning (MRL) approach, optimizing for a set of nested dimensions tailored to your specific needs.
For adaptive retrieval:
1. Perform an initial coarse retrieval using the low-dimensional representation (e.g., 8 or 16 dimensions) to obtain a shortlist of candidates.
2. Iteratively re-rank the shortlist using higher-dimensional representations (e.g., 32, 64, 128, ..., 2048 dimensions) until the desired level of accuracy is achieved.
For adaptive classification:
1. Learn thresholds on the maximum softmax probability for each nested classifier on a validation set.
2. During inference, start with the lowest-dimensional representation and transition to higher dimensions based on the learned thresholds until the desired level of confidence is achieved.

Summary

The beauty of MRL lies in its simplicity and seamless integration with existing representation learning pipelines. By encoding information at multiple granularities within a single vector, MRL empowers researchers and practitioners to strike an optimal balance between accuracy and computational resources, making it a valuable tool in the ever-evolving landscape of machine learning.

Source: https://arxiv.org/pdf/2205.13147

Any opinions in this post are those of the individual author and may not reflect the opinions of AWS.

Site Terms, Privacy, and more.

GenAI under the hood [Part 5] - Matryoshka dolls and Embedding Vectors

What's the connection between these nested Russian dolls and embedding vectors.