Automatic LLM prompt optimization with DSPY

Prompt engineering is the universal fine-tuning step when using generative AI. We always need to write an instruction to use a foundation model. In non-trivial cases, the prompt has a big impact on the ultimate output quality. And of course, if we switch from one model to another, we need to go through the manual prompt crafting process again.

Automatically optimizing prompts for a specific use case is an area of active research. One of the most promising techniques is DSPy, a library for "programming, not prompting, foundation models."

DSPy lets us define a GenAI program or pipeline that captures how we're going to use the foundation model. For example, we can define a program that performs retrieval-augmented generation and uses few-shot prompting. Then DSPy can optimize how this program performs for a specific task. It has several optimizers, ranging from simple ones that optimize few-shot examples, to more complex ones that also optimize the prompt instructions and even model weights.

DSPy has several examples, but they recently added support for foundation models provided in Amazon Bedrock, and that's not immediately clear unless you dig through the documentation. I adapted their simplest working example to use the Mixtral 8x7B model via Bedrock.

First, we just define the foundation model we want to use.

Next, we define our dataset. I'll use one of the ones that DSPy supports out of the box.

Now we define a DSPy module that defines the input and output formats for our task.

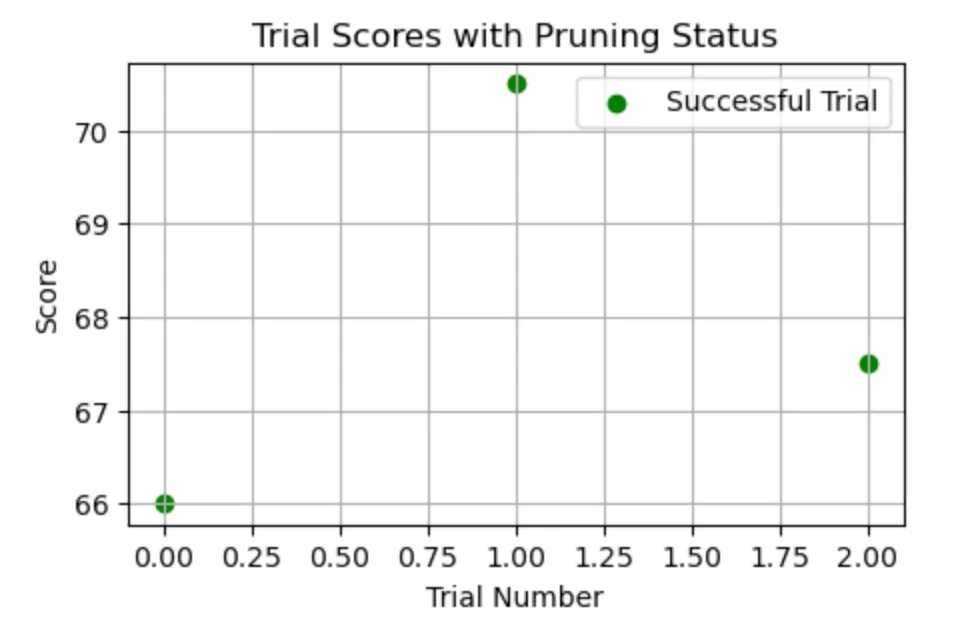
At this point we can run the optimizer. I ran just a handful of trials to save time. I used the MIPRO optimizer as I wanted to optimize the prompt instructions.

In this very simple example, the optimizer started with this base prompt instruction:

During the first trial, it evolved to this prompt instruction.

The best trial ended up with this prompt instruction:

And we can see how the score changed over the course of the three trials.

The DSPy documentation and GitHub site are worth a look. I'd encourage you to give DSPy a try if you want to get the most out of your prompts and foundation models.